2024-10-21 01:32:25 9

【新智元導讀】LLM訓練速度還可以再飆升20倍!英偉達團隊祭出全新架構歸一化Transformer(nGPT),上下文越長,訓練速度越快,還能維持原有精度。
AI的未來,或許就此改寫......
最近,英偉達團隊丟擲的一枚重磅炸彈,提出了全新神經網路架構——歸一化Transformer(nGPT),基於超球面(hypersphere)進行表示學習。
相較於Transformer架構本身,nGPT直接將LLM訓練速度提升至高20倍,而且還保持了原有精度。

也就意味著,原本需要一個月完成的訓練,在未來可能只需1-2天的時間就能搞定。
無疑為通向AGI終極目標,注入了一針強心劑!

論文地址:https://arxiv.org/pdf/2410.01131
在nGPT中,所有的向量(嵌入、MLP、注意力矩陣、隱藏狀態),都被歸一化為單位範數(unit norm)。
輸入後的token在超球面表面上移動,每一層都透過「位移」來貢獻最終的輸出預測,其中位移量是由MLP和注意力模組進行定義的,其向量元件都位於同一個超球面上。
實驗表明,nGPT達到相同精度所需的訓練步驟減少了4-20倍,具體取決於序列長度:
- 1k上下文,訓練速度提高4倍
- 4k上下文,訓練速度提高10倍
- 8k上下文,訓練速度提高20倍

可以看出,上下文越長,訓練越快。
Reddit網友表示,「我很好奇它還能擴充套件到多大程度。如果它能在更長的上下文中大幅擴充套件,這意味著像o1這樣的模型將會獲得顯著的訓練速度優勢」。

還有人表示,「下一代模型將會更高效、更智慧」。

nGPT全新架構,超球面上歸一化
毋庸置疑,Transformer架構是現代大模型的基礎。
不過,當前基於Transformer搭建的大模型都是計算密集型的,需要耗費大量的資源和時間。
為了改進其訓練穩定性、推理成本、上下文長度、魯棒性等方面,AI科學家已進行了大量的修改嘗試。
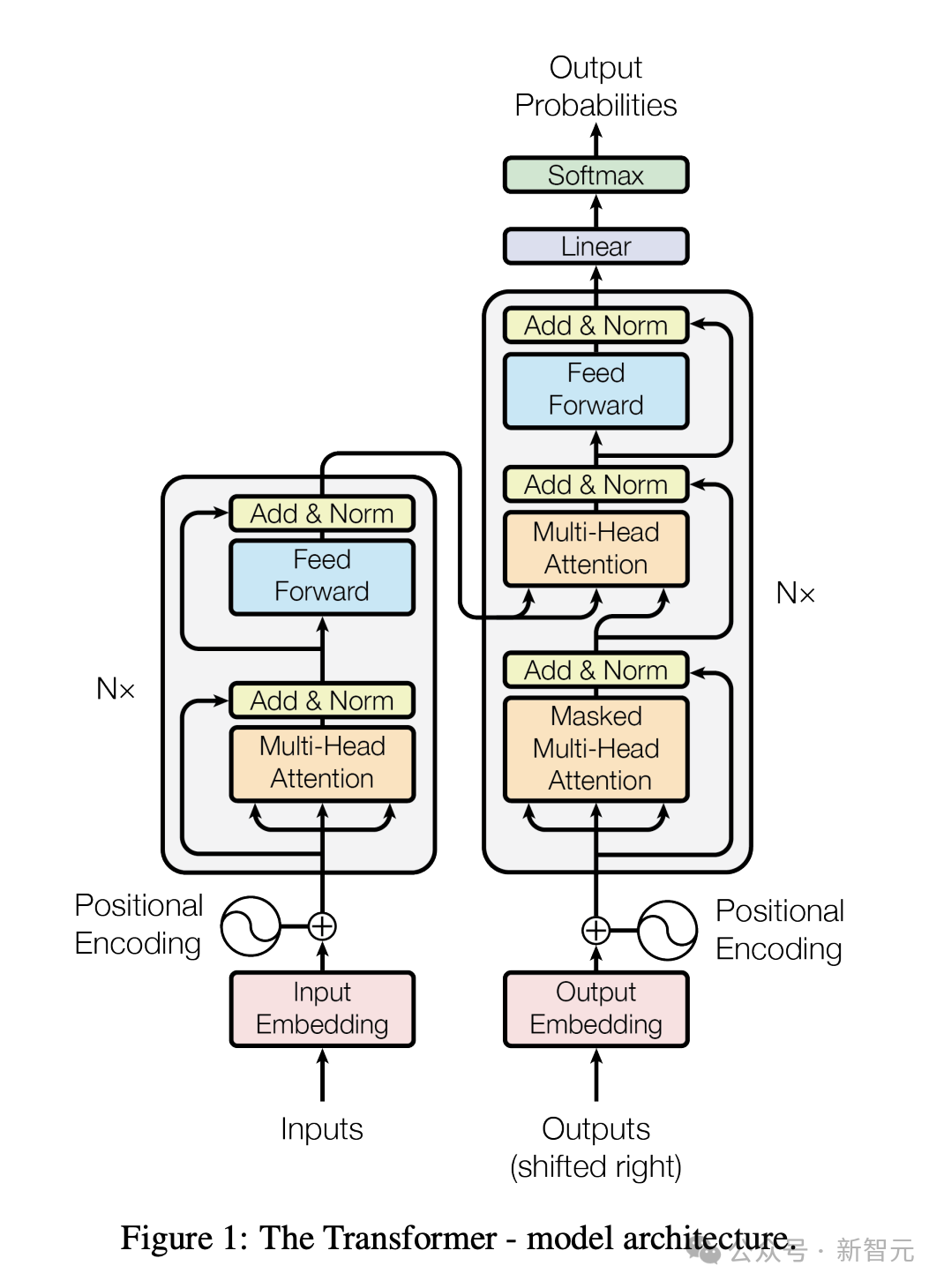
其中,最突出的發現是,歸一化技術對於Transformer效能改善起著重要作用,比如LayerNorm和RMSNorm。
另一種模型歸一化方法是,透過權重衰減(weight decay)控制權重範數。
不過,最新研究又對權重衰減的作用進行評估,並且轉向更多地關注旋轉,而非僅僅關注向量範數。
越來越多的證據表明,在超球面上進行表示學習與更穩定的訓練、更大的嵌入空間可分離性以及在下游任務上的更好效能相關。
而且,還有新研究表明,Transformer隱式地執行梯度下降作為元最佳化器。
由此,英偉達團隊提出了,在歸一化Transformer新視角下,統一該領域的各種發現和觀察。
這項研究的主要貢獻在於:
- 在超球面上最佳化網路引數
建議將形成網路矩陣嵌入維度的所有向量歸一化,使其位於單位範數超球面上。這種方法將矩陣-向量乘法轉化為餘弦相似度的計算,其範圍限定在 [-1,1] 之間。而且歸一化消除了對權重衰減的需求。
- 歸一化Transformer作為超球面上的可變度量最佳化器
歸一化Transformer本身在超球面上執行多步最佳化(每層兩步),其中注意力和MLP更新的每一步,都由特徵學習率控制——這些是可學習的可變度量矩陣的對角線元素。
對於輸入序列中的每個token
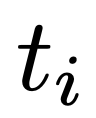
,歸一化Transformer的最佳化路徑從超球面上對應於其輸入嵌入向量的點開始,移動到超球面上最能預測下一個

的嵌入向量的點。
- 更快的收斂
研究證明,歸一化Transformer將達到相同精度所需的訓練步驟減少了4-20倍。
Transformer演變:從GPT到nGPT
嵌入層歸一化
標準的decoder-only Transformer的訓練目標是根據輸入序列的前序tokens來預測後面的token,在token預測時,模型會引入兩個可學習的嵌入矩陣Einput和Eoutput,分別用來從輸入詞轉為詞嵌入,以及從詞嵌入轉為預測輸出。
在模型訓練期間,通常使用對應嵌入向量的點積來計算token相似度,但嵌入向量的範數(norms)不受限制的,可能會導致相似性計算存在偏差。
為了提高相似性估計的準確性,研究人員在新架構中提出,在訓練演算法的每一步之後,對Einput和Eoutput中的嵌入向量進行歸一化。
智慧體在預測文字中的下一個詞時,會使用因果掩碼(casual masking)來確保模型在預測token時不會「偷看」到之後的詞,造成資訊洩露,從而讓模型能夠同時預測多個詞並計算預測誤差,提高訓練效率,同時保持了按順序預測詞的能力。
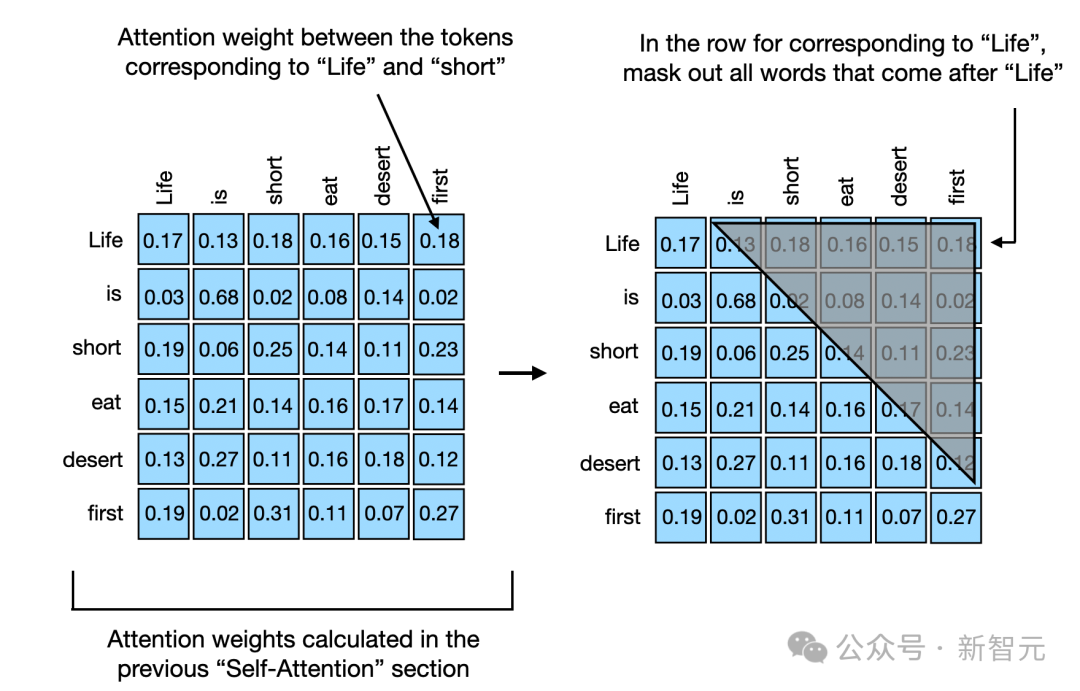
在輸入詞序列後,模型會在預測序列中的每個位置都生成一個輸出向量,然後計算出一個logits向量zi來表示詞彙表中每個詞出現的可能性,可以輔助模型理解不同詞在當前上下文中的重要性:
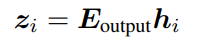
之後用softmax函式把zi轉為機率值,並選取機率最高的詞作為下一個詞的預測。
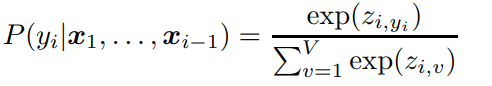
由於nGPT的嵌入矩陣已經歸一化了,所以zi的值範圍為[−1,1],也會限制softmax後得到的機率分佈的置信度,也可以叫做溫度。
為了在訓練過程中調整置信度,nGPT又引入了一個可學習的縮放引數sz,透過逐元素地縮放logits,模型可以更靈活地預測的置信度,更好地學習到在不同情況下如何做出更準確的預測:
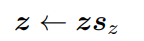
層/塊歸一
標準Transformer架構需要對隱藏層狀態h進行L層變換,包括一個自注意力(ATTN)和多層感知機(MLP)。
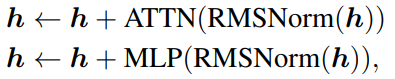
其中RMSNorm也可以替換成其他歸一化(normalization)函式。
隱藏層的引數更新,其實就是在一個超平面上(維度為隱藏層的向量長度)尋找兩個點(原引數和新引數)的最短距離。
1985年,Shoemake提出了球面線性插值(SLERP,Spherical Linear Interpolation),可以沿著球面上兩點之間的最短路徑找到中間點,研究人員發現該方法還可以透過更簡單的線性插值(LERP,linear interpolation)來得到近似解,從而降低計算量:
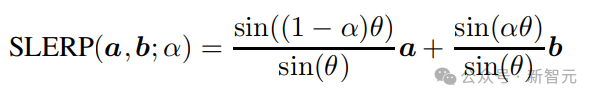
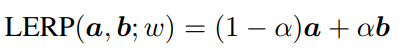
按最短路徑尋找來說,引數更新過程可以描述為:
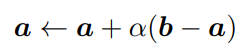
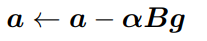
其中a和b是球面上的兩個點,對應到nGPT上,a也就是隱藏層狀態,b是經過注意力機制或MLP塊後的狀態,梯度就是g=a-b,B為可變矩陣。
在擬牛頓方法中,B可以近似於逆黑塞矩陣,當 B是一個對角線元素非負的對角矩陣時,αB就變成了一個向量,其元素對應於B的對角線元素乘以學習率α,也可以稱之為特徵學習率(eigen learning rates)。
eigen源自德語詞,意為「自己的」(own),可以指代Transformer 的內部結構。
所以nGPT中的引數更新方程可以寫為:
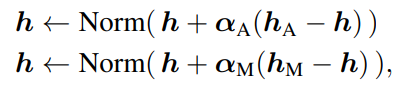
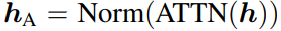
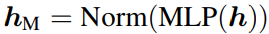
其中αA 和 αM是可學習的引數,分別用於注意力和多層感知機(MLP)模組的歸一化輸出 hA和 hM
與基礎 Transformer 相比,在nGPT的最終層之後不需要再進行額外的歸一化了。
自注意力塊
注意力機制可以說是Transformer中最重要的模組,序列中的每個token都能夠關注到其他所有token,從而讓模型具有捕捉長距離依賴關係的能力。
模型會把處理後的資訊分解成三個部分:查詢(q,query)、鍵(k,key)和值(v,value),可以輔助確定哪些資訊是重要的,以及資訊之間是如何相互關聯的。
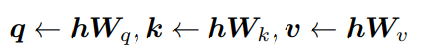
為了確保模型能夠理解每個詞在序列中的位置,模型中通常還會在query和key向量之間加入旋轉位置嵌入(Rotary Position Embeddings,RoPE)。
然後透過計算query向量和key向量的點積、縮放、應用softmax得到注意力權重,對value向量進行加權求和,得到注意力得分。
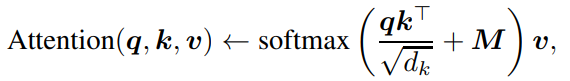
在實踐中,Transformer一般都會用到多個注意力頭,其中每個頭的注意力機制都是獨立計算,最後再透過一個可學習的投影矩陣Wo合併所有頭輸出。
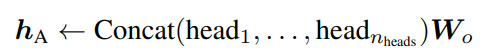
在計算注意力得分的過程中,權重矩陣沒有受到太多限制,可能會導致最終得分過大或過小。
在nGPT中,研究人員對q向量和k向量進行歸一化,還引入了一些可調整的引數(sqk),以確保權重矩陣在處理位置資訊時不會失真,更準確地捕捉到句子中詞與詞之間的關係,從而做出更好的預測和決策。
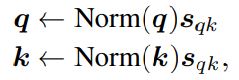
MLP塊
在標準Transformer中,隱藏層收入透過RMSNorm進行歸一化,然後經過兩個線性投影生成中間向量(暫不考慮偏置項):
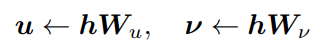
然後使用SwiGLU 門控啟用函式,以及一個線性變換得到最終門控啟用。
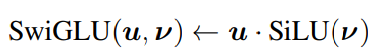
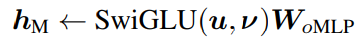
在nGPT中,研究人員提出對線性投影的權重矩陣進行歸一化,並引入可學習的縮放因子,能夠更充分地利用處理資訊時的非線性特性,在處理複雜資訊時更加靈活。
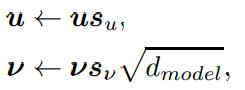
多層感知機模組的輸出不會因為縮放調整而發生變化。
Adam高效學習率
Adam最佳化演算法透過動量和梯度幅度的估計來調整每次的學習步長,同時考慮了當前及過去的梯度資訊。
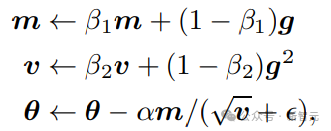
在nGPT中,研究人員同樣引入了一個可訓練的縮放引數向量,對特定的引數進行更精細的控制,確保每個引數都能以最適合自己的速度進行學習,從而進一步提高學習效率。
在不影響全域性學習率的情況下,對特定的引數進行調整,提供了更大的靈活性和控制力。
變化總結
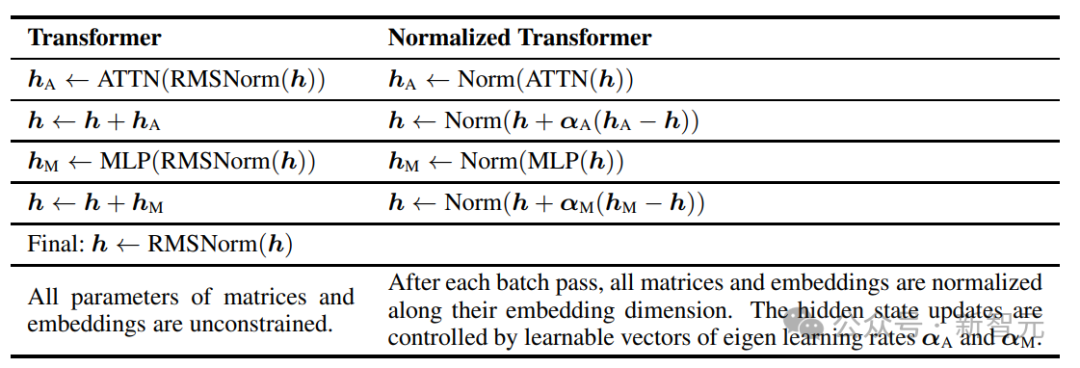
和基礎Transformer相比,nGPT主要做了七個改變:
1、移除所有歸一化層,比如RMSNorm或LayerNorm;
2、在每個訓練步驟之後,沿著嵌入維度對所有矩陣,包括輸入輸出嵌入矩陣,以及各種權重矩陣進行歸一化處理;
3、修改了隱藏層引數更新方程;
4、調整注意力機制中的softmax縮放因子,對q和k進行重新縮放和歸一化;
5、對MLP塊的中間狀態進行重新縮放;
6、對logits進行重新縮放;
7、移除權重衰減和學習率預熱步驟。
上下文越長,訓練速度越快
接下來,研究人員在OpenWebText資料集上訓練了基礎基礎Transformer(GPT)和歸一化Transformer(nGPT),並在一系列標準下游任務上對其進行評估。
實驗中,使用了0.5B和1B(包括嵌入)兩種引數規模的模型。兩種引數規模的模型0.5B和1B(包含嵌入)。

訓練加速
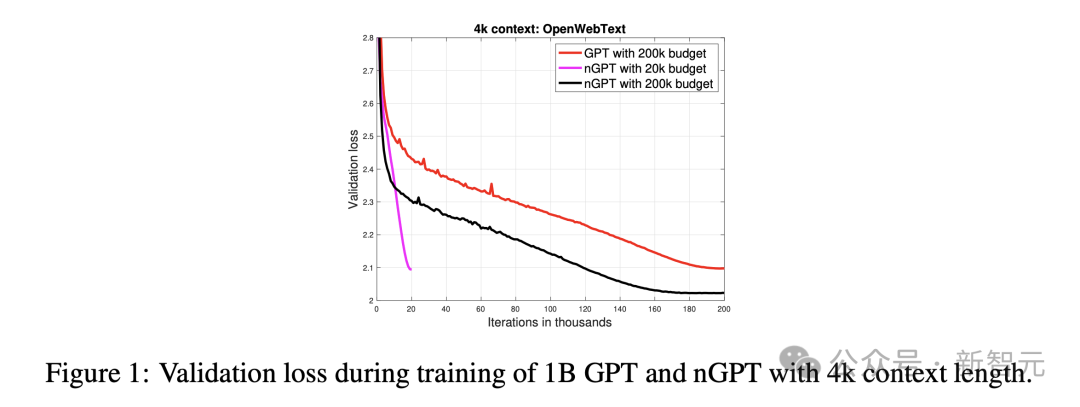
圖1顯示了,在訓練過程中,10億引數且樣本長度為4k token的GPT和nGPT模型的驗證損失。
經過2萬次迭代後,nGPT達到了與GPT在20萬次迭代(約4000億個token)後,才能達到的相同驗證損失。
這表明,在迭代次數和使用token數量方面,nGPT實現了10倍的加速。
再來看圖2,展示了nGPT和GPT在三個方面的效能差距是如何變化的:總token數量、上下文長度、引數規模。
在1k、4k和8k token上下文中,訓練0.5B和1B的nGPT模型分別約快4倍、10倍和20倍。
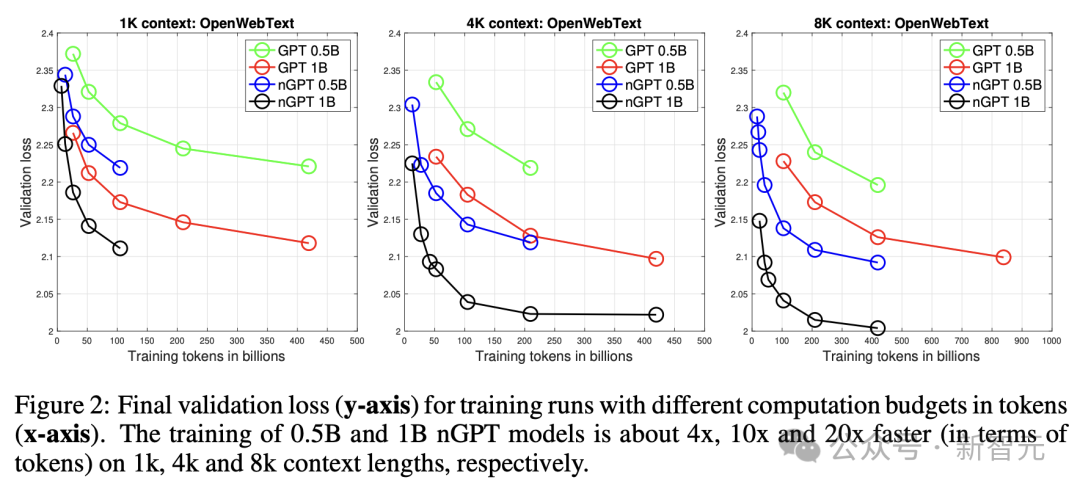
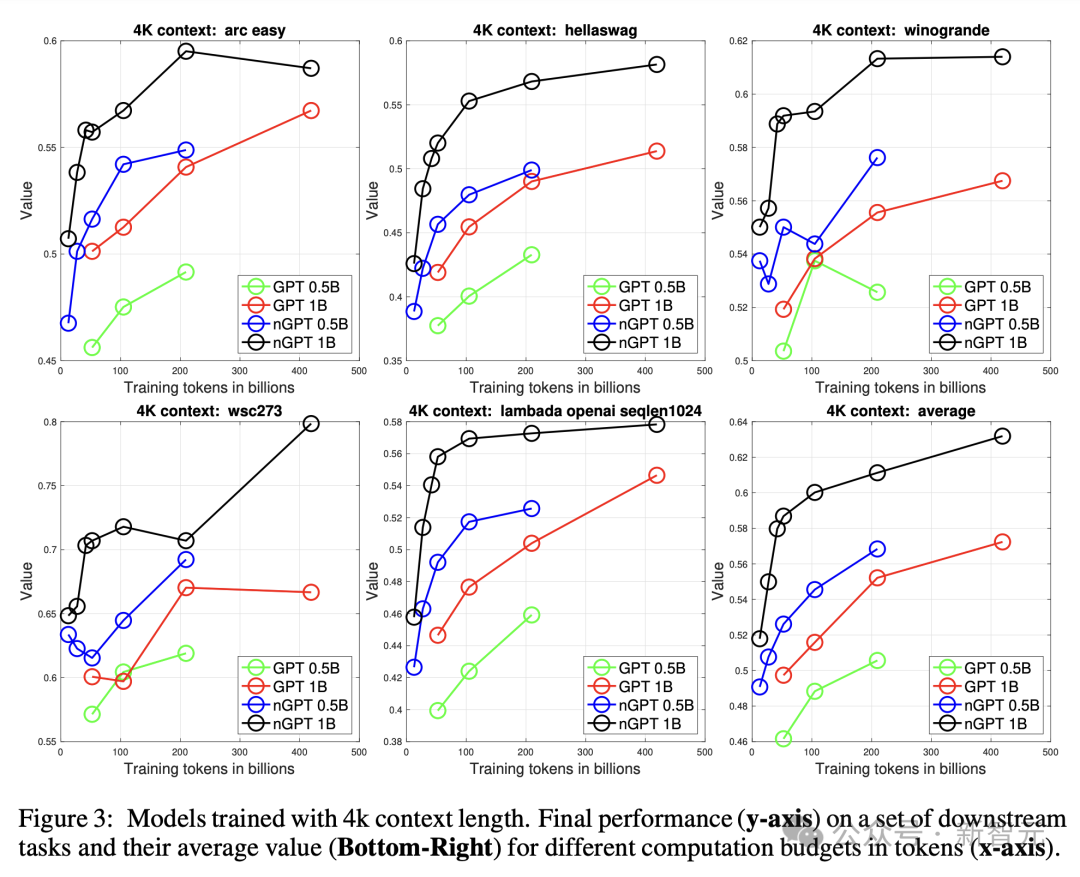
圖3在下游任務中顯示了類似的效能,證實加速不僅反映在困惑度上,也反映在任務表現上。
研究人員觀察到,對於較長的訓練執行,nGPT顯示出一些飽和現象,這暗示在當前可訓練引數數量下,模型容量可能已接近極限。
神經網路引數檢查
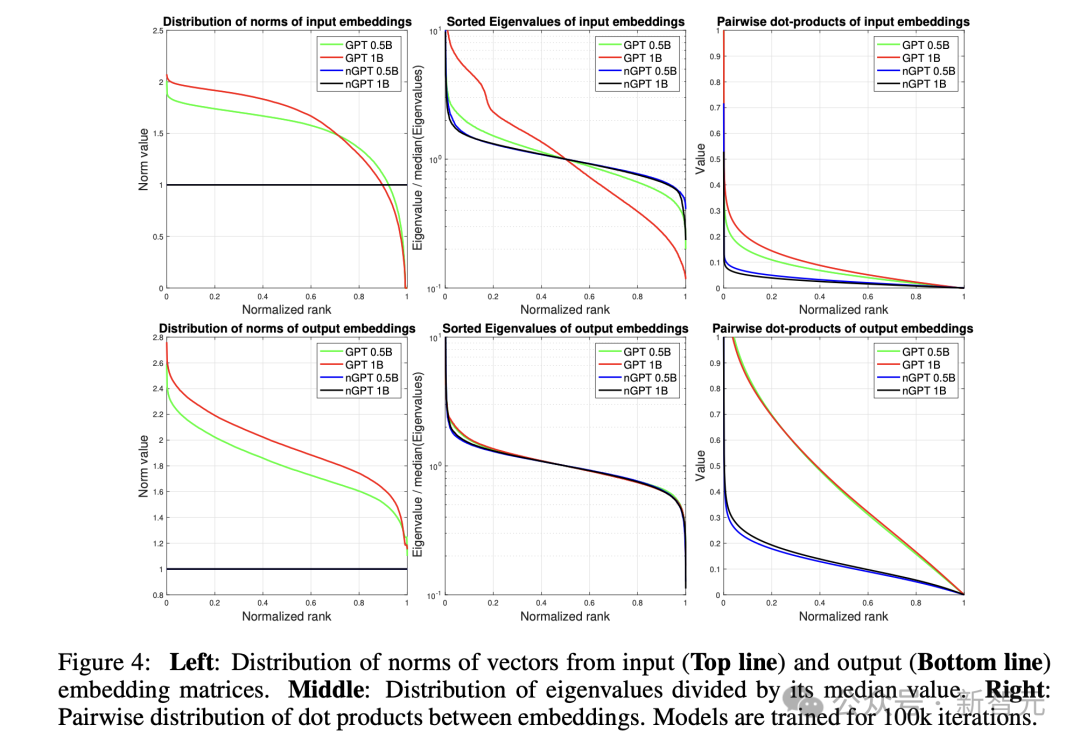
圖4顯示,雖然nGPT保持固定的嵌入範數(這是設計使然),但GPT表現出明顯的變化。
從嵌入的協方差矩陣計算得出的特徵值分佈(已經由其中位數歸一化)顯示,GPT的輸入嵌入具有更高的條件數,尤其是在1B模型中。
嵌入之間的成對點積分佈表明,即使在nGPT中,嵌入也並非均勻分佈在超球面上(在那裡點積會接近0),而是形成簇——這可能反映了語言資料中的自然模式。
由於GPT的嵌入形成了一個超橢球體(hyper-ellipsoid),如向量範數的分佈所示,其點積往往具有更高的值。
GPT輸入嵌入的病態性質(ill-conditioned nature)可能導致涉及這些嵌入的計算問題。
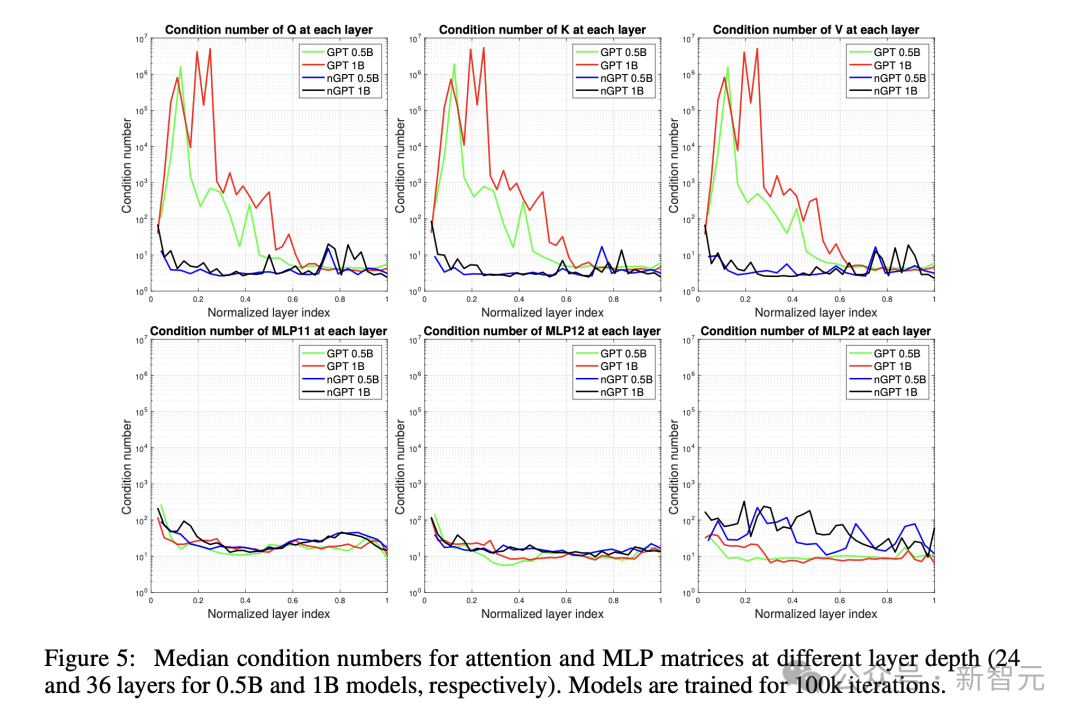
下圖5展示了,注意力和MLP矩陣在不同層深度上的中位數條件數(跨多個頭)——0.5B模型有24層,1B模型有36層。
與nGPT相比,GPT模型的注意力矩陣呈現顯著更高的條件數。
對這些矩陣的進一步檢查,GPT的注意力矩陣表現出退化為低秩矩陣的趨勢,可能減少了這些塊的學習容量。
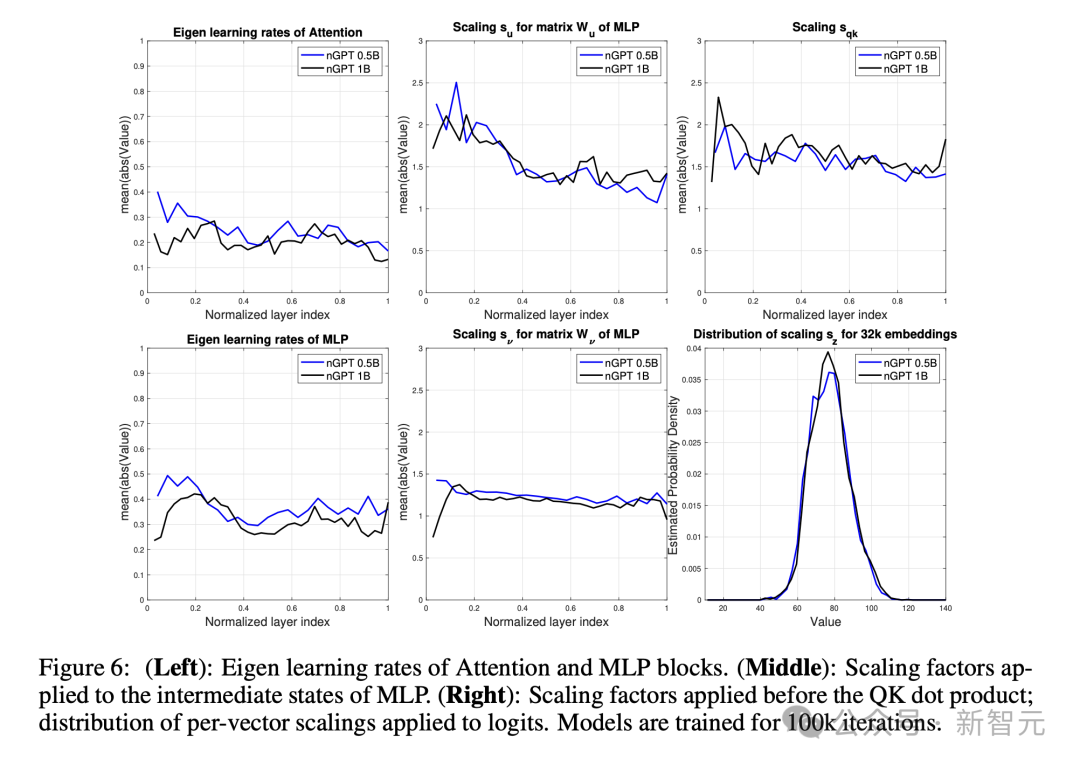
下圖6展示了,(左圖)注意力模組和MLP模組的特徵學習率,(中圖)應用於MLP中間狀態的縮放因子,(右圖)應用於QK點積之前的縮放因子。

2024-10-21 0 人在看

2024-10-21 1 人在看

2024-10-20 2 人在看

2024-10-20 3 人在看

2024-10-20 2 人在看

2024-10-20 2 人在看

2024-10-18 6 人在看

2024-10-18 3 人在看